Attualità

NUMERI E CONGETTURA

FLAVIO VANETTI - 26/11/2021

Tutto dimostrato? Pare proprio di no. Quindi l’ipotesi di Georg Friedrich Bernhard Riemann, il grande matematico e fisico tedesco nato nel 1826 a Jameln e morto a 40 anni in Italia, a Verbania, torna nelle praterie dei grandi problemi irrisolti. Però in queste ore un “rompicapo” che resiste da 150 anni e che nemmeno il suo ideatore era riuscito a verificare ha movimentato le acque della scienza e dei virtuosi dei numeri. Con tanto di giallo. L’agenzia Ansa ha infatti dato la notizia dell’avvenuta soluzione, ad opera dell’italiano Giuseppe Mussardo e del collega André Leclair. Ma pare non sia vero e per la cronaca, se cliccate sul link dell’articolo messo in rete dalla nostra agenzia di stampa, compare la dicitura “error” (provare per credere). A distanza di poche ore, infatti, sono arrivate le smentite nonostante uno studioso, Maurizio Codogno, abbia detto sul suo blog che “la non notizia merita comunque qualche riga”.

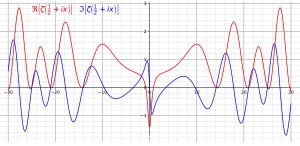
Ma partiamo da quanto è stato annunciato e ci appoggiamo per questo al Quotidiano Nazionale (QN). Ecco come ha formulato la lieta novella: “È stato risolto uno dei più grandi problemi matematici di sempre, che resisteva da 150 anni, e che neanche il suo ideatore era riuscito a dimostrare. Stiamo parlando della congettura (o ipotesi) di Riemann che permette di predire con una grande accuratezza la distribuzione dei numeri primi. E nella coppia di fisici che ha trovato la soluzione del mistero, pubblicata sul Journal of Statistical Mechanics, c’è un italiano, Giuseppe Mussardo della Scuola Internazionale Superiore di Studi Avanzati, che ha lavorato assieme a André Leclair della Cornell University. I due fisici hanno risolto il problema dopo tre anni di lavoro ricorrendo alle nozioni della loro materia: le leggi di probabilità che regolano i movimenti caotici, come quelli degli atomi di gas che si urtano incessantemente fra loro. È stato “un vero tour de force, nell’analisi dati di un insieme incredibilmente grande di numeri primi, i costituenti basi dell’aritmetica, i veri e propri atomi della matematica”, ha spiegato Mussardo. “Al cuore dell’argomento di Riemann c’era una congettura, che però lui non fu in grado di provare, sull’ubicazione di un numero infinito di zeri nel piano complesso di una particolare funzione, nota oggi come la funzione di Riemann” dove gli zeri sembrano allinearsi lungo una linea verticale con una grande regolarità. “Il fatto che la spiegazione venga dalla fisica, ovvero dalla meccanica statistica e dalle sorprendenti connessioni di questa disciplina con un campo genuinamente matematico come quello della teoria dei numeri non fa che svelare la grande unità del sapere scientifico ed aumentare lo stupore di fronte ad un fatto così profondo”.

Nemmeno il tempo di sostenerlo ed ecco la pioggia di contestazioni. Se avete voglia di tuffarvi in un ambiente di numeri e formule, eccovi servita la replica del già citato Codogno (il link è questo). “È noto sin dal Medioevo che la somma degli inversi dei numeri naturali cresce fino all’infinito, anche se con molta calma. La somma degli inversi dei quadrati dei numeri naturali invece ha un valore finito, che Eulero con un po’ di magheggi dimostrò essere π²/6. Nel 1859 il grande matematico tedesco Bernhard Riemann cominciò a prendere la somma degli inversi dei numeri naturali elevati a una potenza qualunque, e generalizzò questa funzione – che in suo onore si chiama la zeta di Riemann – usando potenze che sono numeri complessi. Riemann dimostrò che la sua funzione ζ(s) assumeva il valore zero quando s era un numero negativo pari e per un numero infinito di valori complessi la cui parte reale è compresa tra 0 e 1. Gli sembrava però che quei valori stessero tutti su una retta, quella per cui la parte reale vale esattamente 1/2. Se fosse davvero così, si potrebbe dimostrare che la successione dei numeri primi è sì casuale, ma in un certo senso il meno casuale possibile; in altre parole, la formula li(n) – si legge “logaritmo integrale di n” – che approssima la quantità di numeri primi minori di un qualunque n commette un errore “limitato”. (L’errore c’è, proprio perché i numeri primi si sparpagliano in modo apparentemente strano.) Peccato che in un secolo e mezzo nessuno sia riuscito a dimostrare che gli zeri stanno davvero tutti su quella retta!”. Tutto chiaro, no?